在开启本文之前，请读者们思考一个问题。长度和面积究竟是什么意思？比起数学这貌似更像一个哲学问题。我想，单独回答这个问题是没有意义的，因为长度与面积的仅在于度量。我们说一条线段长度为5之前，必须先给定一段长度为1的标准线段，并用这个1去度量长度5，我们采用的是一种叫做逐段度量的方法，将该线段正好割分为5个标准长度的线段首尾相连。更进一步，如果将线段的长度由5换为类似Π的无理数，我们又是如何测量的？我们采用的方法其实仍是逐段度量的方法，只不过我们是在“尺子”1上加上刻度，用十等分的方法将标准线段不断割成更小段，将其变为0.1，0.01，0.001……，然后依次将它们首尾连接，多进少补，以至于无穷位次，于是便得到了长度。如果我们将之前关于长度的概念提取出来，会发现所谓长度也只不过是用标准长度和适当的度量规则作用后的结果。

不知各位有没有思考过为什么面积等于长×宽，这个公式从小学开始老师便告诉我们它是成立的，却从未对它进行过说明，实际上，它也是来自于度量，如果没有原始的那个 1×1的面积为1的标准方格，我们永远不会知道面积为何物，我们正是用这个标准的格子逐个地对未知的土地进行测量才有了面积的定义。没有测量就没有长度，同样的，没有我们的测量，也就没有面积（或者说我们无法理解面积）。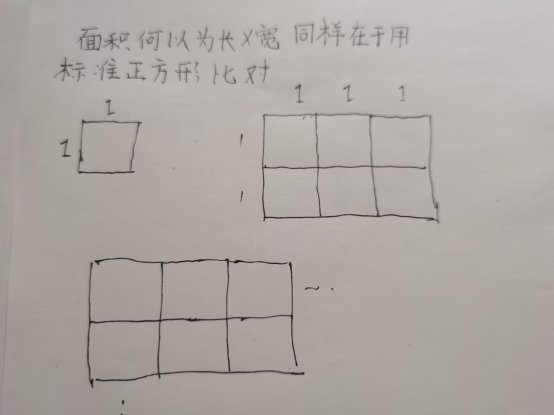

一般的测度概念也不过是在面积和体积的基础上推广了标准尺和测量这两个概念。而标准尺便换成了一般的我们已经熟知的n✖n的立方体，测量方法也从原来的逐段测量变为了外包法。外包法，顾名思义，就是用可数个·n✖n的立方体将所要测量的东西覆盖，再取这些立方体的体积（测度）之和，再对这些和取下确界，便得到了一般图形的所谓的外测度的概念。

既然测度作为体积，面积和长度的推广，那么它自然要满足最基本的几个性质：1.空集的测度为0。   2.可列可加性，即可数个集合的测度的无交并应该等于各自测度之和。 3.平移不变性，即一个集合经过平移以后测度应保持不变。4.这个所谓的测度应和我们之前所理解的面积体积一致，即对于一般的图形如立方体，它的测度应与其体积相同，否则我们的这个推广便成了逻辑上的空洞的东西。这些特性看似十分容易满足，但实际上对其的寻找也很是经历了一番波折，而且最终的结果也未能尽如人意。

然而，可惜的是，外测度并不能对全部的集合满足以上3个性质，事实上，我们可以证明，没有任何定义可以使得所谓的测度满足以上所有性质，也就是说，我们不能找到合适的测度之尺来量取所有的集合。这看起来是一件十分可惜的事如果这样的话，我们对于体积的推广似乎就到此为止了。然而数学很多时候都在从不完美中寻找美。外测度虽然不能使得所有集合都满足那三条，但也可以使得很大一部分集合满足，这便是满足Caratheodory条件的集合，我们　通常称之为可测集。我把它理解为一种妥协，找不到万能测度的遗憾，但这个遗憾本身也已经足够美丽，因为这个遗憾的可测集已经包含了很大一部分集合，如博雷尔集（开集的可列并交叉），更不用说是一般的立方体了。而这样诞生的可测集自身也能完美符合以上的所有要求，我们真正将测度的概念推广到了所有一般图形之上。

那么，我们又为什么要测度这个如此抽象的概念呢？因为积分推广的需要。事实上我们学习测度理论的顺序与数学发展的顺序 是倒过来的，是当时积分有了对一般测度的需要，才催生了现在所谓的勒贝格测度。而勒贝格之所以发展测度理论，也是因为黎曼积分的局限性，连迪利克雷函数这种简单的函数都无法进行积分，与是勒贝格便想到分割y轴而非x轴，但是分割y轴后得到的，是一串也许是简短的点的集合之并，然后用他们乘以函数值得到积分。而这样的想法不可避免地遇到了问题，及对于一般图形的测度有多长的问题，这个时候我们的勒贝格测度也就顺理成章地被派上了用场。而我们以上的关于可测集和测度之所以成立，也不过是因为其能适应积分的需要 。（不好用的推广如Jordan测度早已不是重点讨论的东西）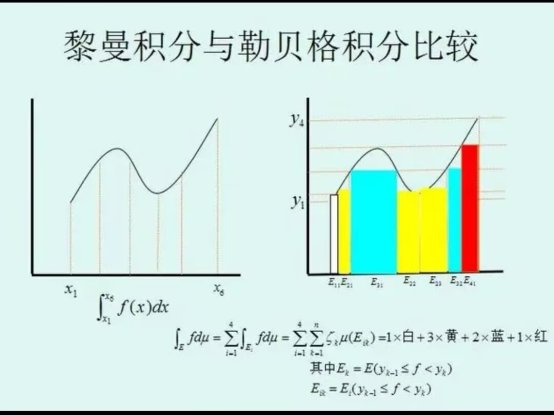

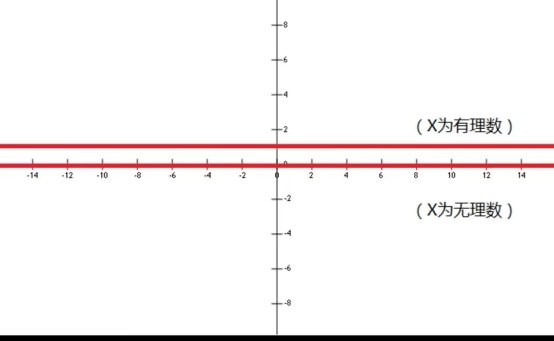
于是，可测集诞生了，在可测集的基础上，分析学的大厦真正建立了起来。